Fastest way to uniquify a list in Python >=3.6

This is an update to a old blog post from 2006 called Fastest way to uniquify a list in Python. But this, time for Python 3.6. Why, because Python 3.6 preserves the order when inserting keys to a dictionary. How, because the way dicts are implemented in 3.6, the way it does that is different and as an implementation detail the order gets preserved. Then, in Python 3.7, which isn't released at the time of writing, that order preserving is guaranteed.

Anyway, Raymond Hettinger just shared a neat little way to uniqify a list. I thought I'd update my old post from 2006 to add list(dict.fromkeys('abracadabra')).

Functions

Reminder, there are two ways to uniqify a list. Order preserving and not order preserving. For example, the unique letters in peter is p, e, t, r in their "original order". As opposed to t, e, p, r.

def f1(seq):  # Raymond Hettinger
    hash_ = {}
    [hash_.__setitem__(x, 1) for x in seq]
    return hash_.keys()

def f3(seq):
    # Not order preserving
    keys = {}
    for e in seq:
        keys[e] = 1
    return keys.keys()

def f5(seq, idfun=None):  # Alex Martelli ******* order preserving
    if idfun is None:
        def idfun(x): return x
    seen = {}
    result = []
    for item in seq:
        marker = idfun(item)
        # in old Python versions:
        # if seen.has_key(marker)
        # but in new ones:
        if marker in seen:
            continue
        seen[marker] = 1
        result.append(item)
    return result

def f5b(seq, idfun=None):  # Alex Martelli ******* order preserving
    if idfun is None:
        def idfun(x): return x
    seen = {}
    result = []
    for item in seq:
        marker = idfun(item)
        # in old Python versions:
        # if seen.has_key(marker)
        # but in new ones:
        if marker not in seen:
            seen[marker] = 1
            result.append(item)

    return result

def f7(seq):
    # Not order preserving
    return list(set(seq))

def f8(seq):  # Dave Kirby
    # Order preserving
    seen = set()
    return [x for x in seq if x not in seen and not seen.add(x)]

def f9(seq):
    # Not order preserving, even in Py >=3.6
    return {}.fromkeys(seq).keys()

def f10(seq, idfun=None):  # Andrew Dalke
    # Order preserving
    return list(_f10(seq, idfun))

def _f10(seq, idfun=None):
    seen = set()
    if idfun is None:
        for x in seq:
            if x in seen:
                continue
            seen.add(x)
            yield x
    else:
        for x in seq:
            x = idfun(x)
            if x in seen:
                continue
            seen.add(x)
            yield x

def f11(seq):  # f10 but simpler
    # Order preserving
    return list(_f10(seq))

def f12(seq):
    # Raymond Hettinger
    # https://twitter.com/raymondh/status/944125570534621185
    return list(dict.fromkeys(seq))

Results

FUNCTION        ORDER PRESERVING     MEAN       MEDIAN
f12             yes                  111.0      112.2
f8              yes                  266.3      266.4
f10             yes                  304.0      299.1
f11             yes                  314.3      312.9
f5              yes                  486.8      479.7
f5b             yes                  494.7      498.0
f7              no                   95.8       95.1
f9              no                   100.8      100.9
f3              no                   143.7      142.2
f1              no                   406.4      408.4

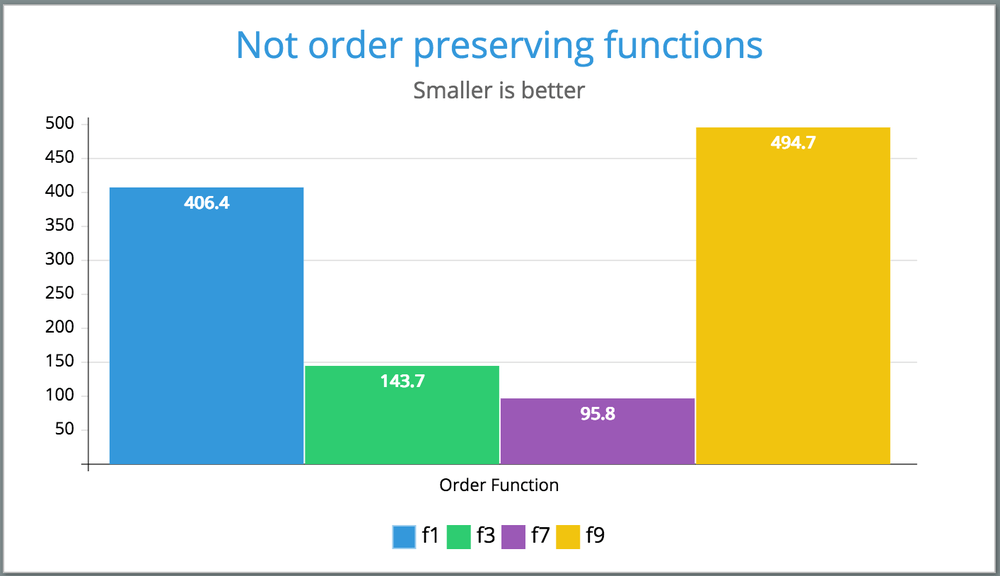
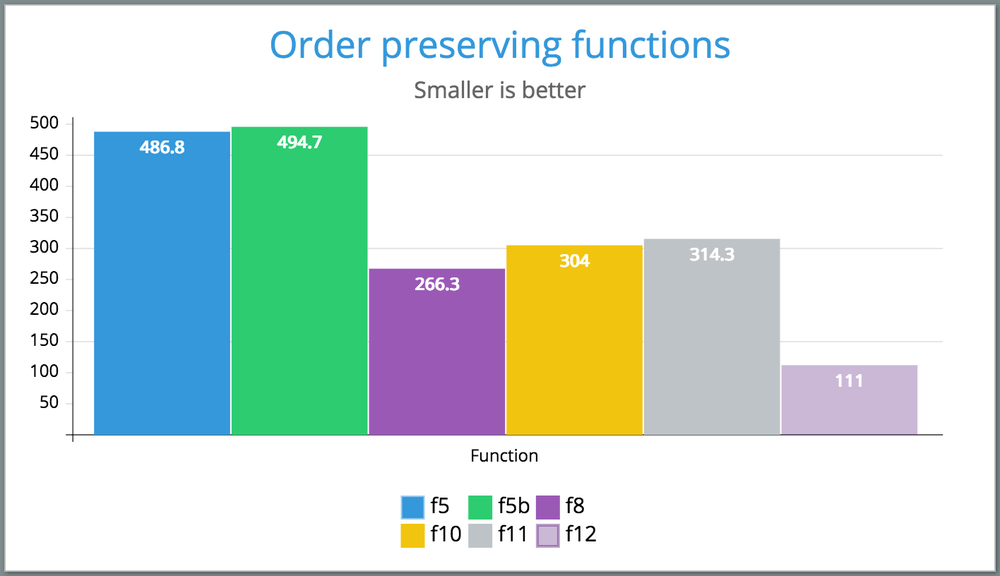
Conclusion

The fastest way to uniqify a list of hashable objects (basically immutable things) is:

list(set(seq))

And the fastest way, if the order is important is:

list(dict.fromkeys(seq))

Now we know.